今天來跟大家聊聊大家常見的指數級別動態規劃從哪裡把時間省下來的~
題目是這樣的,給你一個 2*N 大小的矩形地板空間,你可以用許多 1*2 大小的磚塊去鋪它。
(1) 請問有幾種鋪法呢?
(2) 如果輸入的某些地方有黑影,無法鋪上磚塊,請問有幾種鋪法呢?
第一個問題可以用數學方法解決,而且會得到費氏數列的結果。
第二個問題也可以用數學方法解決並證明,而且會得到許多費氏數列項乘起來的結果。
如果今天換成了 3*N 大小的矩形地板空間,我們仍用 1*2 大小的磚塊去鋪它。此時回答第一個問題便有些吃力。倘若使用動態規劃,我們勉強可以歸納出幾種不同的型態:

注意到最右邊的邊界,如果我們定義 dp(n, type ∈ {1, 2, 3}) 代表已經由左至右鋪到 n 排、且最後一排的長相如同上面三種情形之一(允許上下顛倒相同類型)。那麼我們可以列出遞迴式子:
dp(n, 1) = dp(n-2, 1) + dp(n-1, 3) (解釋:最右邊那排三個都是橫放、或至少有一塊直放)
dp(n, 2) = dp(n-1, 1) + dp(n-1, 3) (解釋:用一塊直放把它消掉、或用兩塊橫放消掉)
dp(n, 3) = dp(n-1, 2) (解釋:最右邊那個只能放一塊橫的)
於是就可以做出動態規劃囉!這個方法可以解決 (1),如果要解決 (2),則會多出第四和第五種情況:就是中間一格凸出、或中間一格凹下。這樣寫出遞迴式子會更加麻煩。
雖然我們最終能順利寫出遞迴關係,但要推廣 3*N 鋪磚塊問題到 K*N 鋪磚塊問題實在是太困難了——因為對於同一個 n 而言,情況的總數可能會高達 2^K 種,轉移的方法也可能有 1.618^K 種啊。遞迴轉移處理起來也實在是很令人困擾。而且時間複雜度可能高達 K*N*(2*1.618)^K。
前述的動態規劃方法中,我們一次考慮一排、試圖依次往前推進一整排。這樣會因為狀態總數和狀態的轉移跟據列數指數級別增加,不太妥當。如果我們放寬條件,從每一排按照順序一格一格往下考慮。在考慮該格的時候,我們可以用拼圖的方式放上四種拼圖的任何一塊:

那只要所有紅色邊框的位置互相貼齊相鄰格子,就可以保證其鋪磚塊的正確性!那我們的狀態會變成什麼樣子呢?看看邊界的地方,與尚未確定的格子交接的地方也只有邊界呀。其他格子到底怎麼鋪其實一點也不重要~所以我們可以把邊界從上到下編碼成長度為 K+1 的二元字串:010100。其中 1 的地方是未來可能需要有相接處的。於是目標函數的定義就可以是 dp(row, col, 現在邊界的編碼) = 滿足現在邊界狀況到底可以有幾種放 (row, col) 這格的方式?此時可以推敲出轉移是常數時間的。因此時間複雜度跟狀態總數一樣: O(K*N*2^(K+1))。
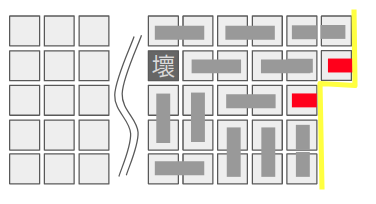
把一個拉很長的東西表示成一格一格把東西鋪上去的方法,其實還滿巧妙的~
而且「這個邊界」的概念,可以延伸到固定樹寬(Tree-width)的各種圖上的組合最佳化問題,相當有用呢。終於快要抵達30天了,希望可以繼續寫,好的我們明天見~

我有找到 K*N 的實作方式,不過還是無法理解.. 崩╰(〒皿〒)╯潰
https://cp-algorithms.com/dynamic_programming/profile-dynamics.html
想請問樓主,dp[x][mask] 指的是,從 row 1 一路鋪到 row x,滿足 mask 的條件之下有幾種放法,這樣的理解對嗎?假設 K = 2, N = 4, 如果 row = 2, next_mask = 1100 b,那合法的 mask (row = 1) 好像只有 0011 b (row = 1) (我有把中間過程印出來),可是為什麼 0011 b (row = 1) 會跟 1100 b (row = 2) 有關係?我不懂 next_mask 跟 mask 的關係,以及為什麼 for loop 是從 mask = 0 開始,而不是從 mask = 1111 b 開始 QQ
// g++ -O3 -g -std=c++11 dp.cpp
#include <iostream>
#include <vector>
using namespace std;
int row, col;
vector<vector<uint64_t>> dp;
void calc(int x, int y, int mask, int next_mask) {
if (y == col) {
dp[x + 1][next_mask] += dp[x][mask];
} else {
int my_mask = 1 << y;
if (mask & my_mask)
calc(x, y + 1, mask, next_mask);
else {
calc(x, y + 1, mask, next_mask | my_mask);
if (y + 1 < col && !(mask & (my_mask << 1)))
calc(x, y + 2, mask, next_mask);
}
}
}
uint64_t countTiling(int numRow, int numCol) {
row = numRow, col = numCol;
dp.clear();
dp.resize(row + 1, vector<uint64_t>(1 << col));
dp[0][0] = 1;
for (int x = 0; x < row; ++x) {
for (int mask = 0; mask < (1 << col); ++mask)
calc(x, 0, mask, 0);
}
return dp[row][0];
}
struct TestPattern {
uint8_t numRow, numCol;
uint64_t ans;
TestPattern(uint8_t r, uint8_t c, uint64_t ans)
: numRow(r), numCol(c), ans(ans) {}
};
int main(int argc, char *argv[]) {
bool fail = false;
vector<TestPattern> testPatterns = {{7, 16, INT64_C(3710708201969)},
{7, 15, INT64_C(0)},
{8, 17, INT64_C(4841110033666048)},
{8, 10, INT64_C(1031151241)}};
for (const auto &p : testPatterns) {
uint64_t ans = countTiling(p.numRow, p.numCol);
if (ans != p.ans) {
cout << "Failure: (" << (int)p.numRow << ", " << (int)p.numCol
<< "), expect = " << p.ans << ", get = " << ans << endl;
fail = true;
}
}
if (!fail)
cout << "success verified!\n";
return 0;
}